A mixed bag: the cost per vote story

A while ago I wrote an article in Campaigns and Elections with a friend about cost per vote. The idea was to demystify some of the discussion around the relationship between campaign expenditure and winning votes. This post takes the time to unpack some of those ideas even more and provide an updated framework for thinking about everyone's favorite metric.

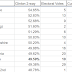
To get everyone up to speed, here’s the straightforward approach to calculating CPV:

Imagine that you’re running a race for school board and you want to use some of the money in your campaign coffers to turn out some voters. You decide to send mail, but since you want to learn something for your future campaigns, you hold out a control group. You send 1,000 pieces of mail to a random selection of voters and don’t send mail to a control group of the same size. On election day 540 people who received your mail voted and 520 people in the control group voted. This gives you a treatment effect of 2% (+20 votes / 1000 people.) Now suppose that you paid $500 to send those 1000 pieces of mail: you wind up with $500 / 20 votes: which is a cost per vote of $25.

Now that we're on the same page about what CPV is, it’s time to tear it down so we can build it back up. First, we have to understand cost per vote in the context of winning an election. The goal of optimizing around CPV is not to find the intervention that nets you the most votes for the fewest dollars, but rather to assemble a set of interventions that get you to a win as cheaply as possible. This is a hugely important distinction and where a lot of tacticians get hung up. Below are some examples that help to highlight this distinction and get you thinking in CPV:

Never gonna win:
Imagine that you’re a Democrat running for congress in Wyoming where in 2018 the Republican won by more than a 2:1 margin (127k votes for the Republican to 60k votes for the Democrat) Now let's say that you have some absolutely killer intervention that gets you 100 votes for $5. That’s not to say that for every $5 you put into the machine you get 100 votes, but rather that you have an intervention that you can deploy once that will cost $5 and will generate 100 votes. A CPV of $0.05 is unheard of and seems like a no brainer, but if you go from losing by 68k votes to 67.9k votes you still lose the election by a wide margin. Does this mean that the $5 was wisely spent or no?

The close but not so close case:
Imagine now that you’re a Republican staffer working in a competitive senate election against an incumbent Democrat. All of the signs point to your state being one of the most competitive races on the map. Because this is going to be such a close race, you deploy every tactic that you can think of since it’ll come down to a narrow margin. You even hold out a control group and measure the effect sizes of your interventions so you can evaluate everything after the race. Then your candidate says something monumentally stupid-- like the kind of stupid that operatives will talk about eight years later-- and support for your candidate drops by 10 percentage points. This drop moves everyone you persuaded back to supporting the Democrat and a whole bunch of other voters move away as well. Did the CPV on the tactics you deployed change? Was this a wise investment at the time you made it?

The truly close race:
Now let's think about a race where the bottom doesn’t fall out. The race is close and stays close. In fact, it’s so close that it’s won by exactly 1 vote. Just like the previous example, you deployed all of the tactics and after the election you have a range of CPVs for your tactics. If you were able to generate 100 votes for an investment of $1,000 in digital ads and you were able to generate another 100 votes from an investment of $10,000 in direct mail, would you go back and spend all the money that you spent on direct mail in digital ads? Should we say that direct mail is a worse investment than digital ads?

The chopping block:
Finally let's imagine that you’re a campaign manager in a competitive race and you’re responsible for the campaign’s budget. You have $35,000 that you can use to add to a flight of persuasion mail you’ve already tested or you can hire a press assistant. The value of the mail is known-- you tested it and that additional $35,000 will generate 700 votes (CPV of $50) and the value of a press assistant (in terms of votes) is unknown, but relationships with journalists will suffer and this might result in your candidate being portrayed less favorably in the media. This will cost you votes, but how many votes it will cost you is unclear. What’s the better bet, and how would you make the call?

Diminishing Returns and CPV

Next, let's talk about diminishing returns on tactics. We don't know the exact function for diminishing returns on campaign interventions, but we’ve got a reasonable idea about the shape of the curve. I’m going to present 4 campaign tactics and show how even when we start with wildly different CPV for the first intervention we want to start mixing in other tactics pretty quickly.

Here I’ll assume that every tactic has the same diminishing returns rate and they all follow the function 1/(2^n) * ATE (average treatment effect.) If we start with the following assumptions about cost and effect size for each tactic, we get CPV curves in the chart below:

Tactic	Cost	Effect	CPV
GOTV Mail	$0.35	1.00%	$35.00
Digital pre-roll	$0.02	0.20%	$10.00
Canvass	$5.00	5.00%	$100.00
TV	$0.03	0.20%	$15.00

Now the effect sizes and costs are going to be off here, but the general shape of what’s going on should be consistent with what someone doing this with a richer data set. There is a really wide gap for the first intervention between expensive and cheap tactics, but pretty quickly the first intervention at an expensive tactic starts out-performing additional interventions on the cheap tactics.

If you want to be a stickler about this, the diminishing returns curves probably re-start for every new piece of creative (e.g. a new mailer or a new tv/digital ad) but in my experience even with new creative, we are still subject to diminishing returns within any mode, though we move more slowly up that curve if creative is changed more frequently. My best guess here is that there’s a ceiling on application (e.g. many people don’t read their mail or use an ad blocker) and another ceiling on new information (e.g. once someone has heard a thing before, the next intervention is met with “i know that already!”)

The Ark and the Clown Car

Ok so now that we’re stuck in nihilistic impotence, it’s time to talk about how to actually make decisions using CPV. As I discussed in the “never gonna win” scenario (and will continue to discuss at every opportunity,) the driving factor for everything is whether or not the race is competitive. If the race will not be competitive, your CPV does not matter because elections are winner-take-all. If you’re coming from commercial marketing, increasing market share from 25% to 30% is as good as increasing market share from 47.5% to 52.5%, but in elections those are worlds apart. So we’re only talking about competitive races.

Now that we are in the world of competitive races, the next thing to consider is budget. As we saw in the “close but not so close” example, you’re going to deploy your budget as if your race was close and hope for the best. This means that you’re not setting some vote goal based on where support is right now and asking what tactics you use to get close the gap and reach your target number of votes. There might be big shocks that cause swings in support levels, so building from a top-down approach like “we need to generate 8,000 votes to secure a win” is just going to lead to weird and brittle decisions. So now we’re to a point where we’re talking about competitive races and starting from a budget.

Once we have our budget, the goal is to assemble a set of interventions that will deliver the most votes. This is where the decisions are going to be driven more by judgement than by formal evidence, but I’ll try to describe how to navigate them. The most principled approach I can come up with is by dividing expenditures into ones that are subject to diminishing returns and ones that benefit from increasing returns. Things like door-to-door canvassing, direct mail, and other direct marketing tactics all seem to be subject to diminishing returns. Things like opposition research, flacking, and community organizing seem to benefit from increasing returns. My best guess about why this happens is that the direct marketing tactics are unable to benefit from network effects because they’re delivered in an atomized way that doesn’t allow for communication around a shared experience (just a guess though!)

So we’ve got these two bins-- interventions that are subject to diminishing returns and interventions that benefit from increasing returns. We’ll start with the diminishing returns bin, where we should check all the boxes at low levels. That means doing a little bit of everything to make sure that all of our interventions are at their most potent. Specifically this means that if the budget allows it, every reasonable tactic should be on the table for it’s first pass. We should then move up our CPV curve for each of the cheapest tactics until we have matched the CPV of our most expensive tactic’s first pass because by investing in the most expensive tactic we're stating that we're comfortable with a CPV that's at least that high. Using the interventions from our diminishing returns curve above, that means our budget would look like:

Tactic	Cost	Passes	Marginal CPV
GOTV Mail	$0.35	2	$70
Digital pre-roll	$0.02	4	$80
Canvass	$5.00	1	$100
TV	$0.03	3	$60

Here our marginal CPV is our CPV for the last application before we cross over into our next most expensive tactic. So the first GOTV mailer had a CPV of $35 and the second one had a CPV of $70. Just to be very explicit about this, I’m not recommending this exact mix-- mixing depends on more robust diminishing returns calculations by mode, more precise estimates of ATE and the best price you can get for your interventions. I’m only using these made up data as an example. What’s essential to understand here, though, is that campaigns benefit from a diversity of tactics. This should be like Noah’s ark-- don’t bring a lot of anything, but get as many different species on as possible.

Once we get out of direct marketing tactics, things get a lot more complicated. Funding the increasing returns bins is largely untouched in the academic lit, but if you ask experts things like campaign communications, research, and community organizing are among the most essential components of an election. Interventions in these bins should look more like a clown car than the ark-- pack as many people in as possible until no else can fit.

So when we're building our budget we start by checking all the boxes for our tactics and filling up on them until we start getting crushed by diminishing returns and then pack all the rest of the money into the clown cars. 

Where, what, who: a sorting exercise

In my last post I talked about why it’s crucial to allocate proportional to tipping point to underscore that the where a campaign places its resources is the most important tactical decision that a campaign can make. This post proposes a framework for rank-ordering what types of tactical decisions campaigns prioritize with the goal of hopefully shifting some focus away from sorting lists of voters and drawing additional focus on testing interventions.

A Brief History Lesson

For folks who aren’t familiar, microtargeting is what we call the development of lists of specific voters who the campaign should communicate with to win their votes. Below is the canonical example of how campaigns think about microtargeting:

Lets first walk through what the chart is telling us and then we can talk about some deeper implications from this chart. This chart tells us that campaigns want to turn out voters who are likely to support a candidate conditional on voting, but are unlikely to vote. This chart also tells us that campaigns want to persuade people who are very and somewhat likely to vote and have medium support levels. So we turn out the people that support but don't often vote, and persuade the people that frequently vote but are on the fence about who to support. Easy enough?

What this approach is really trying to do is maximize the net votes gained from a campaign contact. For turnout communications (interventions that increase the likelihood of voting,) campaigns do better to increase participation among people who support the candidate-- if you convince 100 people who wouldn’t otherwise vote to show up on election day, you don’t net any votes unless these hundred people are more likely to support your candidate than the opponent. Similarly if you can only persuade 100 people to support your candidate, you’d rather the people you persuade actually show up and vote than skip the election after you do all the work of persuading them to support your candidate. So far things hold up and are largely correct.

Where this breaks down is in selecting only medium supporting voters to persuade. You could make an argument about ceiling effects being too severe for persuading voters with high support, but preventing defection is equivalent to persuading votes, so that argument doesn’t really hold water. Similarly, you could make an argument that people with really low support are never going to support your candidate, but losing a group by 70/30 instead of 80/20 has the same impact on net votes as going from losing a group 45/55 to winning a group 55/45 so that doesn’t stand up either. Fortunately folks have largely moved on to thinking about sorting lists of who receives persuasion communication by likelihood to respond to an intervention (sometimes called uplift targeting or heterogeneous treatment effects modeling.)

And this gets to the heart of what this post is about. Sorting lists is less important than getting the intervention right and both are less important than getting the map right. The Where > What > Who paradigm is something that many practitioners miss for a host of reasons. I speculate that the biggest reason folks get this wrong is because “Who” is optimized with fancy statistics that can be learned, so you can be “good” at it-- “What” on the other hand is largely about luck (though there may be some raw talent component?) and doesn’t allow for the same kind of expert identity.

Rather than speculate on why campaign practitioners focus on "who" so much, I'll get to the point-- getting the intervention right is far more important than getting the targeting right.

Debunking the importance of "who"

To set up this analysis, I’m going to generate a bunch of fake interventions with a mean of 0.5 percentage points. Two thirds of the time, we’ll set our standard deviation to  0.25 percentage points and one third of the time we’ll set our standard deviation to 1 percentage point-- put another way, two thirds of the time, the variation is small and one third of the time the variation is big. The distribution of treatment effects for our intervention looks like this:

The shape of this distribution is largely in line with commercial advertising estimates in that there's a pretty tight distribution with a mean close to 0 and a pretty small share of big winners and losers. I’m going to use these data to randomly draw an intervention and compare the average treatment effect (ATE) for a selected intervention that is well targeted (e.g. it hits the most treatment responsive voters) vs. the average treatment effect from the best intervention selected through testing. 

To perform this analysis, we’re going to have to make some assumptions about the heterogeneity of treatment effects (HTE). After previewing this post with a couple of close friends, I think it's worth taking a moment to talk about the distribution of heterogeneous treatment effects and how the shape of that distribution affects our prioritization. Below is a chart of 5 ways that HTEs could be distributed across a population for an intervention with an ATE of 0.5pp:

I used 2 axes here because the the treatment effects vary so wildly based on what we assume about their distribution. The bars on this chart use the right hand axis and the lines use the left hand axis. Here's what each one means:

• Extreme HTE (blue): Here the treatment only moves the top 1% of the population (100% treatment effect no less) and that the bottom 1% backlash at a 50%. For everyone else in the population this has no effect. I've never seen anything like this, and all the examples I can construct look like doctors giving the wrong person medicine.
• Linear HTE (red): Here we see a proportional and linear increase in treatment effect across the full population. The top half of the population responds positively to the treatment and the bottom half responds negatively. I've never seen anything like this either, but you can probably construct an example that involves an economist making a zero-sum game.
• Root HTE (yellow): Here we see a treatment effect that behaves kind of like the linear treatment, but the effects are much more muted since the HTE is the square root of population share. In the this example, the treatment effect among the most responsive 10% of the population is ~3x as large as the average treatment effect and the bottom 10% backlashes at ~-3x the ATE. I've seen treatment effects behave like this when a campaign is communicating on a really polarized issue like guns or abortion.
• Normal HTE (green): This is just a normal distribution of the treatment effects with a standard deviation that is as big as our main effect (0.5pp.) This produces some variation in both enrichment and backlash, but the overwhelming majority of the population has a treatment effect close to the main effect. This is the most common shape of treatment effect distribution that I've seen.
• Uniform HTE (orange): This is just what it looks like when there's no treatment heterogeneity. It's a flat line across the full population. This happens far more often than you might expect, though it rarely shows up when machine learning methods that are prone to over-fitting are used to estimate HTEs.

So now we can make some comparisons. The chart below compares the average treatment effect when you test multiple interventions vs. the heterogeneous treatment effect when you target your intervention. Since the chart has a lot going on, so let me break it down: 

• Solid lines show HTE sizes for percentile of the population.
• Dashed lines show ATEs for the full population.
• Y axis is the average treatment effect.
• X axis is the percentile of the population (e.g. for HTEs, treatment effects are larger at the 90th percentile than the 10th percentile.) 

What does this tell us? In most cases-- like when treatment effects are normally or uniformly distributed-- testing 2 interventions does better than targeting the most treatment responsive voters. In cases when there is very strong treatment heterogeneity (the square root case) we see that figuring out who to target beats pre-testing because most people aren't moved by the treatment and there's a proportional positive and negative effect at both extremes. Additionally, for all of the assumptions about treatment heterogeneity that we considered, just testing 3 interventions and picking the best one dominates once you get past the top 25% of the population. 

If what we’re looking to do is maximize our treatment effect for campaign interventions, it’s pretty clear that trying more stuff and picking the winner yields more votes than trying to suss out which voters are most responsive to campaign communications and hitting them with the first intervention off the shelf. This places getting “what” right firmly ahead of getting “who” right in terms of how campaigns allocate their research resources. If a campaign wants to figure out who to communicate with, at the very least it's worth explicitly stating the assumptions of the exercise. Some examples of stating these hidden assumptions are:

• I believe that treatment effects for our interventions will have a normal distribution with a very small standard deviation (this implies that treatments will all have pretty similar effect sizes and that there aren't big winners or losers"
• I believe that treatment effects will be extremely heterogeneous, with some amount of backlash and most of the movement happening in a small share of the population.
• I believe that the cost of detecting heterogeneous treatment effects for an intervention (this requires a much bigger sample size) is a better use of resources than testing more interventions.
• I believe that groups that we've found to be acutely responsive to interventions in the past are going to continue to be the most responsive groups to new interventions, so we can continue to target based on past research.

To be very clear about this, I disagree with all four of these statements. I think that the spread on treatment effects across interventions is pretty large, that the differences within the population in treatment responsiveness to political communications are often very small, the cost of detecting HTEs is usually worth less than the cost of finding a better intervention, and that when we find big treatment heterogeneity it's often not extensible to other interventions.

Tying this back to last week’s post, the most pivotal decision a campaign can make is getting resources into the tipping point state. Once resources are allocated into the tipping point state, it’s more important to figure out what to do than it is to figure out who to do it to. 

Where > What > Who.