Where, what, who: a sorting exercise

In my last post I talked about why it’s crucial to allocate proportional to tipping point to underscore that the where a campaign places its resources is the most important tactical decision that a campaign can make. This post proposes a framework for rank-ordering what types of tactical decisions campaigns prioritize with the goal of hopefully shifting some focus away from sorting lists of voters and drawing additional focus on testing interventions.

A Brief History Lesson

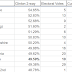
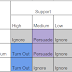
For folks who aren’t familiar, microtargeting is what we call the development of lists of specific voters who the campaign should communicate with to win their votes. Below is the canonical example of how campaigns think about microtargeting:

Lets first walk through what the chart is telling us and then we can talk about some deeper implications from this chart. This chart tells us that campaigns want to turn out voters who are likely to support a candidate conditional on voting, but are unlikely to vote. This chart also tells us that campaigns want to persuade people who are very and somewhat likely to vote and have medium support levels. So we turn out the people that support but don't often vote, and persuade the people that frequently vote but are on the fence about who to support. Easy enough?

What this approach is really trying to do is maximize the net votes gained from a campaign contact. For turnout communications (interventions that increase the likelihood of voting,) campaigns do better to increase participation among people who support the candidate-- if you convince 100 people who wouldn’t otherwise vote to show up on election day, you don’t net any votes unless these hundred people are more likely to support your candidate than the opponent. Similarly if you can only persuade 100 people to support your candidate, you’d rather the people you persuade actually show up and vote than skip the election after you do all the work of persuading them to support your candidate. So far things hold up and are largely correct.

Where this breaks down is in selecting only medium supporting voters to persuade. You could make an argument about ceiling effects being too severe for persuading voters with high support, but preventing defection is equivalent to persuading votes, so that argument doesn’t really hold water. Similarly, you could make an argument that people with really low support are never going to support your candidate, but losing a group by 70/30 instead of 80/20 has the same impact on net votes as going from losing a group 45/55 to winning a group 55/45 so that doesn’t stand up either. Fortunately folks have largely moved on to thinking about sorting lists of who receives persuasion communication by likelihood to respond to an intervention (sometimes called uplift targeting or heterogeneous treatment effects modeling.)

And this gets to the heart of what this post is about. Sorting lists is less important than getting the intervention right and both are less important than getting the map right. The Where > What > Who paradigm is something that many practitioners miss for a host of reasons. I speculate that the biggest reason folks get this wrong is because “Who” is optimized with fancy statistics that can be learned, so you can be “good” at it-- “What” on the other hand is largely about luck (though there may be some raw talent component?) and doesn’t allow for the same kind of expert identity.

Rather than speculate on why campaign practitioners focus on "who" so much, I'll get to the point-- getting the intervention right is far more important than getting the targeting right.

Debunking the importance of "who"

To set up this analysis, I’m going to generate a bunch of fake interventions with a mean of 0.5 percentage points. Two thirds of the time, we’ll set our standard deviation to  0.25 percentage points and one third of the time we’ll set our standard deviation to 1 percentage point-- put another way, two thirds of the time, the variation is small and one third of the time the variation is big. The distribution of treatment effects for our intervention looks like this:

The shape of this distribution is largely in line with commercial advertising estimates in that there's a pretty tight distribution with a mean close to 0 and a pretty small share of big winners and losers. I’m going to use these data to randomly draw an intervention and compare the average treatment effect (ATE) for a selected intervention that is well targeted (e.g. it hits the most treatment responsive voters) vs. the average treatment effect from the best intervention selected through testing. 

To perform this analysis, we’re going to have to make some assumptions about the heterogeneity of treatment effects (HTE). After previewing this post with a couple of close friends, I think it's worth taking a moment to talk about the distribution of heterogeneous treatment effects and how the shape of that distribution affects our prioritization. Below is a chart of 5 ways that HTEs could be distributed across a population for an intervention with an ATE of 0.5pp:

I used 2 axes here because the the treatment effects vary so wildly based on what we assume about their distribution. The bars on this chart use the right hand axis and the lines use the left hand axis. Here's what each one means:

• Extreme HTE (blue): Here the treatment only moves the top 1% of the population (100% treatment effect no less) and that the bottom 1% backlash at a 50%. For everyone else in the population this has no effect. I've never seen anything like this, and all the examples I can construct look like doctors giving the wrong person medicine.
• Linear HTE (red): Here we see a proportional and linear increase in treatment effect across the full population. The top half of the population responds positively to the treatment and the bottom half responds negatively. I've never seen anything like this either, but you can probably construct an example that involves an economist making a zero-sum game.
• Root HTE (yellow): Here we see a treatment effect that behaves kind of like the linear treatment, but the effects are much more muted since the HTE is the square root of population share. In the this example, the treatment effect among the most responsive 10% of the population is ~3x as large as the average treatment effect and the bottom 10% backlashes at ~-3x the ATE. I've seen treatment effects behave like this when a campaign is communicating on a really polarized issue like guns or abortion.
• Normal HTE (green): This is just a normal distribution of the treatment effects with a standard deviation that is as big as our main effect (0.5pp.) This produces some variation in both enrichment and backlash, but the overwhelming majority of the population has a treatment effect close to the main effect. This is the most common shape of treatment effect distribution that I've seen.
• Uniform HTE (orange): This is just what it looks like when there's no treatment heterogeneity. It's a flat line across the full population. This happens far more often than you might expect, though it rarely shows up when machine learning methods that are prone to over-fitting are used to estimate HTEs.

So now we can make some comparisons. The chart below compares the average treatment effect when you test multiple interventions vs. the heterogeneous treatment effect when you target your intervention. Since the chart has a lot going on, so let me break it down: 

• Solid lines show HTE sizes for percentile of the population.
• Dashed lines show ATEs for the full population.
• Y axis is the average treatment effect.
• X axis is the percentile of the population (e.g. for HTEs, treatment effects are larger at the 90th percentile than the 10th percentile.) 

What does this tell us? In most cases-- like when treatment effects are normally or uniformly distributed-- testing 2 interventions does better than targeting the most treatment responsive voters. In cases when there is very strong treatment heterogeneity (the square root case) we see that figuring out who to target beats pre-testing because most people aren't moved by the treatment and there's a proportional positive and negative effect at both extremes. Additionally, for all of the assumptions about treatment heterogeneity that we considered, just testing 3 interventions and picking the best one dominates once you get past the top 25% of the population. 

If what we’re looking to do is maximize our treatment effect for campaign interventions, it’s pretty clear that trying more stuff and picking the winner yields more votes than trying to suss out which voters are most responsive to campaign communications and hitting them with the first intervention off the shelf. This places getting “what” right firmly ahead of getting “who” right in terms of how campaigns allocate their research resources. If a campaign wants to figure out who to communicate with, at the very least it's worth explicitly stating the assumptions of the exercise. Some examples of stating these hidden assumptions are:

• I believe that treatment effects for our interventions will have a normal distribution with a very small standard deviation (this implies that treatments will all have pretty similar effect sizes and that there aren't big winners or losers"
• I believe that treatment effects will be extremely heterogeneous, with some amount of backlash and most of the movement happening in a small share of the population.
• I believe that the cost of detecting heterogeneous treatment effects for an intervention (this requires a much bigger sample size) is a better use of resources than testing more interventions.
• I believe that groups that we've found to be acutely responsive to interventions in the past are going to continue to be the most responsive groups to new interventions, so we can continue to target based on past research.

To be very clear about this, I disagree with all four of these statements. I think that the spread on treatment effects across interventions is pretty large, that the differences within the population in treatment responsiveness to political communications are often very small, the cost of detecting HTEs is usually worth less than the cost of finding a better intervention, and that when we find big treatment heterogeneity it's often not extensible to other interventions.

Tying this back to last week’s post, the most pivotal decision a campaign can make is getting resources into the tipping point state. Once resources are allocated into the tipping point state, it’s more important to figure out what to do than it is to figure out who to do it to. 

Where > What > Who.